
Die piezoelektrische Ladungskonstante
Bisher haben wir uns eher mit den qualitativen als mit den quantitativen Aspekten des Piezo-Effekts befasst. Um auch eine quantitative Übersicht zu erhalten, benötigen wir Zahlen, zum Beispiel um Materialien zu vergleichen oder um die Empfindlichkeit eines Accelerometers zu berechnen.
Die Zahl, die angibt, wie gut das Material eine mechanische Kraft in eine elektrisches Ausgangssignal umwandelt, wird als piezoelektrische Konstante bezeichnet.
Am wichtigsten für unsere Anwendungen ist die piezoelektrische Ladungskonstante d .
Sie ist gleich der erzeugten Ladung geteilt durch die aufgebrachte Kraft d=Q/F.
[d] = pC / N (pico-Coulomb pro Newton)
Q ist die elektrische Ladung [Q] = pC (pico Coulombs)
F ist die mechanische Kraft [F] = N (Newton)
Die Dimension von d ist
Streng genommen ist diese einfache Gleichung nur dann richtig, wenn keine anderern Einflussfaktoren vorhanden ist. Das bedeutet zum Beispiel, dass die Temperatur konstant bleibt und nur eine einzige Kraft auf den Piezo wirkt.
Richtungs-Indizes (Subskripte)
-
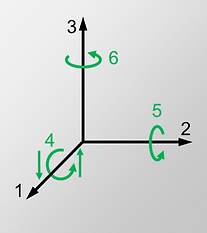
Die Richtungen von x, y und z der Kraft und des elektrischen Feldes werden durch 1, 2 und 3 dargestellt.
-
Die Scherspannung, die um die Achsen 1, 2 und 3 auftritt, wird durch die Zahlen 4, 5 und 6 dargestellt.
Eine Scherzustand liegt vor, wenn wir zwei entgegengesetzte Kräfte anwenden, die dazu neigen, den Körper in dem durch die Zahlen 4, 5 und 6 angegebenen Sinne zu drehen.
Die Indizes (Subskripte) i und k bedeuten:
Bezeichnung der Achsen
i k
d
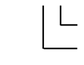
k = Richtung der mechanischen Einwirkung
i = Richtung des elektrischen Feldes
(= Richtung senkrecht zu den Elektroden)
Beispiele für Subskripte
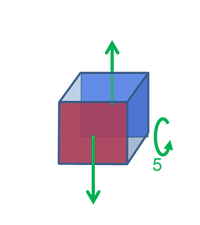
Kompressions-Modus .
d33 gibt die elektrische Ladung (pC) an, die in 3-Richtung erzeugt wird (Elektroden senkrecht zur Achse 3)
pro Newton (N) Kraft, die auch in 3-Richtung auf den piezoelektrischen Körper ausgeübt wird.
( Bewege den Mauszeiger über das Bild, um eine Kraft auszuüben)



Transversaler Modus
d31 ist die elektrische Ladung (pC), die an Elektroden senkrecht zur Achse 3 erzeugt wird
pro Newton (N) Kraft, die in der 1-Richtung angewendet wird.


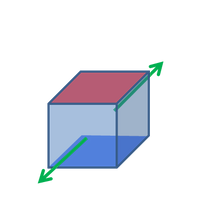
Schermodus
d15 bedeutet, dass die elektrische Ladung in der 1-Richtung entwickelt wird (Elektroden senkrecht zur Achse 1)
pro aufgebrachter Einheit Scherspannung 5
( 5 = Scherung um die 2-Achse, dh Aufbringen einer Kraft nach unten an der Vorderseite des Teils, während es auf der Rückseite gehalten wird)


In der Literatur oder in den Materialdatenblättern findet man d normalerweise mit zwei Indizes dik
Die Indizes i und k geben an, in welcher Richtung i des Piezokristalls die elektrische Ladung auftritt, während wir eine Kraft in Richtung k aufbringen ( i unterscheidet sich möglicherweise von k ).
Um Richtungen in einem piezoelektrischen Element zu identifizieren, werden drei rechtwinklig aufeinander stehende Achsen verwendet. Diese Achsen werden anstelle der klassischen Achsen x, y und z mit 1, 2 und 3 bezeichnet.
Empfindlichkeit eines Piezoelements
Wenn wir eine piezoelektrische Konstante verwenden, ist es oft die Empfindlichkeit eines Piezoelementes, die wir wirklich wollen.
Dh die elektrische Ladung Q wenn wir eine bestimmte Kraft F aufbringen.
Wir erinnern uns, die Ladungskonstante d ist gleich der Ladung geteilt durch die Kraft.
d = Q / F oder Q = d · F (wir brauchen nur das passende dik )
Wir wissen, dass die Ladung über die Oberfläche verteilt ist. Dies könnte zu dem Eindruck führen, dass eine Vergrösserung der Oberfläche auch die Ladung erhöhen würde. Wenn wir dies tun, wird die Kraft jedoch auch über eine grössere Fläche verteilt und die Spannung pro Fläche wird dann im gleichen Verhältnis kleiner.
Dies bedeutet, dass die Ausgangsladung unabhängig von der Grösse des Piezoelements ist.


