Übersicht
Bisher haben wir uns nur mit qualitativen Merkmalen des Piezoeffekts befasst. Um auch eine quantitative Analyse durchführen zu können, benötigen wir Zahlen, zum Beispiel um Materialien zu vergleichen oder um die Empfindlichkeit eines Accelerometers zu berechnen.
In der Welt der Piezoelektrizität werden meist die folgenden Symbole verwendet:
E = elektrisches Feld
D = elektrische Verschiebung
T = mechanische Spannung
S = mechanische Dehnung
s = elastische Nachgiebigkeit, der inverse Wert des Elastizitätsmoduls Y (s = 1/Y)
ε = Permittivität (manchmal wird der Buchstabe K für die relative Permittivität verwendet)
d = piezoelektrische Ladungskonstante
g = piezoelektrische Spannungskonstante
k = Kopplungskoeffizient
Die Zahl, die den piezoelektrischen Effekt eines Materials quantifiziert, wird als piezoelektrische Konstante bezeichnet. Am wichtigsten für unsere Anwendungen ist die piezoelektrische Ladungskonstante d, die angibt, wie gut das Material mechanische Beanspruchung in elektrische Ladung umwandelt.
d = P / T die Dimension von d ist [d] = C / N (Coulomb pro Newton)
oder [d] = pC / N (pico Coulomb pro Newton)
P ist die Polarisation [P] = C / m²
T ist die mechanische Spannung [T] = Pa = N / m²
Die piezoelektrische Ladungskonstante d ist gleich der erzeugten Polarisation P pro Einheit der mechanischen Spannung T, der ein piezoelektrischen Körper ausgesetzt wird.
Diese einfache Gleichung ist jedoch nur dann korrekt, wenn die Temperatur konstant bleibt, das anfängliche elektrische Feld gleich Null ist und wenn ein einachsiger Spannungszustand herrscht. Das heisst eine einachsige Zug- oder Druckspannung oder eine einachsige Scherung.
(Detailiertere Angaben findest du auf der roten Seite.)
Ein interessantes Detail der Ladungskonstante wird deutlich, wenn wir ihre Dimension betrachten: Sie ist unabhängig von der Oberfläche, was bedeutet, dass die Ladung, die wir von einem piezoelektrischen Körper erhalten, nur von der Kraft abhängt, die wir anwenden, nicht von der Grösse des Oberfläche!
Richtungs-Indizes (Subskripte)
-
Die Richtungen von x, y und z für allgemeine Grössen werden durch 1, 2 und 3 dargestellt
-
Die Scherspannung um die Achsen 1, 2 und 3 wird durch die Zahlen 4, 5 und 6 dargestellt
-
Bei Piezokeramiken ist die Richtung der positiven Polarisation in der Regel die 3-Achse. (unter Kompression ist die Polarität der Ladung identisch mit der des ursprünglichen Polarisationsfeldes)
Die Indizes (Subskripte) i und k bedeuten:
i k
d
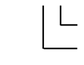
k = Richtung der mechanischen Beanspruchung
i = Richtung des elektrischen Feldes
= Richtung senkrecht zu den Elektroden
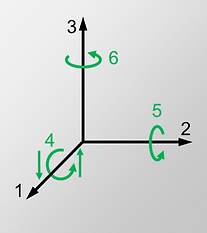
Achsen zur Spezifizierung der piezoelektrischen Konstanten
Beispiele für Subskripte
Piezoelektrische Ladungskonstante dik [C / N]
Kompressions-Modus (Longitudinal-Modus)
d33 gibt die in der Richtung 3 erzeugte Polarisation pro mechanischer Zugspannungseinheit (T ) an, die in der 3-Richtung auf den piezoelektrischen Körper einwirkt.
( Bewege den Mauszeiger über das Bild, um eine Kraft aufzubringen.)
Transversal Modus
d31 ist die in der 3-Richtung erzeugte Polarisation pro Spannungseinheit, die in der 1-Richtung ausgeübt wird
(alle anderen externen Spannungen = 0).
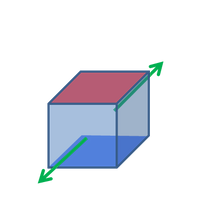
Scherungs-Modus
d15 bedeutet die in der 1-Richtung erzeugte Polarisation pro aufgebrachter Einheit Scherspannung 5 (= Scherung um die 2-Achse), wenn keine anderen externen Spannungen vorhanden sind.
Hinweis: Die oben genannten mechanischen Einwirkungen sind uniaxial. Alle anderen mechanischen Einflüsse (Scherung oder Kompression) sind gleich Null.
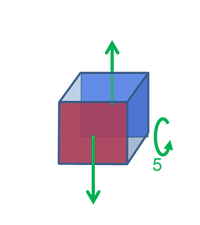
Piezoelektrische Spannungskonstante gik [Vm / N]
g31 ist das elektrische Feld, das in der 3-Richtung entsteht, pro Spannungseinheit die in der 1-Richtung angelegt wird (wenn keine anderen äusseren Spannungen vorhanden sind).
Die Beziehung zwischen der Spannungskonstante und der Ladungskonstante ist
d=εᵀg oder g=d/εᵀ
Das hochgestellte T (Superscript) zeigt an, dass dieser Wert bei konstanter Spannung T gilt
Kopplungskoeffizient kik [./.]
k13 bezeichnet den Kopplungskoeffizienten zwischen dem mechanischen Energieeintrag in Richtung 1 und der umgewandelten Energie in Richtung 3 oder umgekehrt.
Der elektromechanische Kopplungsfaktor k ist das Mass für die Wirkungsgrad, mit der ein piezoelektrisches Material elektrische Energie in mechanische Energie oder mechanische Energie in elektrische Energie umwandelt.
converted energy
k² = –––––––––––––
input energy
Inverser Piezoeffekt dik [m / V]
d33 ist die Dehnung in 3-Richtung pro Einheit des in 3-Richtung angelegten elektrischen Feldes, wobei der piezoelektrische Körper mechanisch frei ist und die elektrischen Felder in 1- und 2-Richtung gleich Null sind.
In der Literatur und Material-Datenblättern findet man d in der Regel mit zwei Richtungs-Indizes dik
Aufgrund der anisotropen Natur der piezoelektrischen Materialien sind ihre Eigenschaften (Elastizität, Permittivität, Ladungskonstante usw.) richtungsabhängig. Mathematisch werden sie als Tensor-Grössen bezeichnet. Aus diesem Grund werden die Konstanten mit zwei Subskripten geschrieben, die sich auf die Richtung der betreffenden Grösse beziehen.
Die Richtungen in einem piezoelektrischen Element werden mit drei orthogonalen Achsen 1, 2 und 3 bezeichnet, analog zu x, y und z des klassischen dreidimensionalen Achsenkreuzes.
Materialkonstanten und Zustands-Superscripte
In der Literatur oder in Datenblätter findet man Ausdrücke wie sᴰ, sᴱ, εᵀ, εˢ usw. Sie bedürfen einiger weiterer Erläuterungen. Die Superskripts (Hochzahlen) zu den Symbolen bezeichnen nämlich die in den Randbedingungen konstant gehaltene Grösse.
Beispiele von Zustands-Superscripten
sᴱ11 = Nachgiebigkeit für eine (Zug-)Spannung und zugehörige Dehnung beide in Richtung 1
bei konstantem elektrischen Feld (= Elektroden kurzgeschlossen).
sᴰ36 = Nachgiebigkeit bei Scherung um die Achse 3 und entsprechende Dehnung in Richtung 3
bei konstanter elektrischer Verschiebung (= offener Stromkreis der Elektroden)..
εᵀ11 = Dielektrizitätskonstante, dielektrische Verschiebung und elektrisches Feld in Richtung 1
bei konstanter mechanischer Spannung (= mechanisch frei)..
εˢ33 = Dielektrizitätskonstante in Richtung 3
bei konstanter Dehnung (= mechanisch eingespannt).
Empfindlichkeit eines Piezoelements
Wenn wir eine piezoelektrische Konstante verwenden, ist es meistens die Empfindlichkeit, die wir wirklich wollen. Dh die elektrische Ladung Q oder die Spannung V , die wir erhalten, wenn wir eine bestimmte Kraft F aufbringen.
Wir erinnern uns, die Ladungskonstante d ist die Polarisation P durch die mechanische Spannung T
d = P / T.
P = Q / A (elektrische Ladung pro Oberfläche)
T = F / A (mechanische Belastung pro Oberfläche)
daher
d = Q / F oder Q = d · F (wir brauchen nur das passende dik )
Wir wissen, dass die Ladung über die Oberfläche verteilt ist, Dies könnte zu der Annahme führen, dass eine Vergrößerung der Oberfläche auch die Ladung erhöhen würde. Wenn wir dies jedoch tun, wird die Kraft ebenfalls über eine grössere Fläche verteilt und die Spannung wird proportional kleiner. Wie wir bereits gesehen haben, ist die Ausgangsladung unabhängig von der Grösse des Piezoelements.
Um die Spannungsempfindlichkeit zu berechnen, wird es etwas komplizierter. Wir können die Spannung über die Kapazität des Piezoelements erhalten.
Die Spannung U eines Kondensators C ist U = Q / C.
Das Piezoelement ist ein Plattenkondensator
mit der Oberfläche A und der Dicke t .
Die Kapazität C ist dann
C = ε · A / t
dadurch wird die durch die Kraft F erzeugte Spannung
d · F · t
U = –––––––––
ε · A
und mit d/ε = g U = g · F · t / A
Wir sehen, dass der erste Teil der Gleichung analog zur Ladungsformel ist, die aber als Erweiterung den „Formfaktor“ t / A enthält.
Die Ausgangsspannung ist daher abhängig von Grösse und Form des Piezoelements!
Der pyroelektrische Effekt
Einige der piezoelektrischen Kristalle und alle Piezokeramiken besitzen auch im ungespannten Zustand eine ausgeprägte Polarachse. Dies führt zu einer Änderung der Polarisation und des Auftretens einer elektrischen Ladung an der Oberfläche, wenn der Piezo einer Temperaturänderung ausgesetzt wird. Dies wird als pyroelektrischer Effekt bezeichnet. Der pyroelektrische Koeffizient p ist definiert als die Änderung des spontanen Polarisationsvektors P mit der Temperatur T.
p = d P / dT
p ist ebenfalls ein Vektor und die skalare Einheit ist [p] = C· m⁻² · K⁻¹
Die spontane Polarisation dieser Piezomaterialien ist also nicht konstant, sondern variiert mit der Temperatur. Wenn wir zum Beispiel das Kristallgitter von PZT betrachten, können wir uns vorstellen, dass das positive Zentrum (rot) seine relative Position in Bezug auf die negativ geladenen Sauerstoffatome (grün) geringfügig ändert, wenn der Kristallit einer anderen Temperatur ausgesetzt wird.
Der gesamte pyroelektrische Koeffizient, der bei konstanter Spannung (= mechanisch frei) auftritt, ist die Summe eines primären pyroelektrischen Effekts, der bei konstanter Dehnung bestehen würde
(= mechanisch blockiert), und eines sekundären pyroelektrischen Effekts, der auf die thermische Ausdehnung des Piezomaterials zurückzuführen ist.
Das bedeutet, dass der pyroelektrische Effekt in Wirklichkeit eine quasi statische Ladung ist, die in einem festen Verhältnis zur Temperatur steht. Es bleibt die Frage, warum wir ihn nur während einer Temperaturänderung beobachten können. Das liegt daran, dass der Innenwiderstand des Piezoelements nicht unendlich ist und ein kleiner Strom von einer Elektrode zur anderen fließt und die pyroelektrischen Ladungen dabei wieder verschwinden. Bei einer Temperaturänderung hat die Ladung jedoch nicht die nötige Zeit, um zu verschwinden.