

Piezo Accelerometer Tutorial
Was ist Vibration?
Vibration
Man sagt ein Körper vibriert, wenn er als Ganzes oder Teile davon um eine Ruheposition schwingen.
Für den Moment betrachten wir nur Schwingungen die periodisch (oder zyklisch) sind.
Die Anzahl der Schwingungen (Zyklen), die während 1 Sekunde ausgeführt werden, heisst Frequenz.
Die Dimension der Frequenz nennt man Hertz (Hz).
1 Hz ist gleich 1/sec (oder 1 Schwingung pro Sekunde).
Wenn eine oszillierende Bewegung aus einer einzigen Komponente mit einer festen Frequenz besteht (wie zu Beispiel bei einer Stimmgabel), dann spricht man von einer harmonischen oder sinusförmigen Schwingung.
Die Vibrationen einer reellen Maschine sind normalerweise viel komplexer und bestehen aus mehreren Komponenten, die gleichzeitig auftreten.

Heinrich Hertz © by Wikipedia, the free encyclopedia
Drei verschiedene Arten Vibration zu beschreiben
Im Folgenden werden wir die sinusförmige Schwingung genauer untersuchen. Es gibt drei verschiedene Möglichkeiten, die Vibration zu beschreiben und zu quantifizieren: Schwingweg, Geschwindigkeit und Beschleunigung.
Schwingweg (Displacement)
Die über die Zeitachse generierte Kurve wird als Sinus bezeichnet, wobei
D = Amplitude
= grösster Ausschlag
(positiv oder negativ)
T = Periode
= Zeit für einen kompletten Zyklus
f = Frequenz f = 1/T
= Anzahl Schwingungen pro Sekunde

Geschwindigkeit (Schwinggeschwindigkeit)
Die Schwinggeschwindigkeit ist eine weitere Art zur Beschreibung der Schwingung.
Die Schwinggeschwindigkeit ist auch eine Sinusfunktion. Sie eilt jedoch dem Schwingweg um die Phasenverschiebung voraus*.
Die Phasenverschiebung beträgt 1/4 einer Periode.
Man sagt auch der Phasenwinkel ist = 90°
(die ganze Periode entspricht 360°)
V = Geschwindigkeits-Amplitude
Frequenz f = 1/T
*) Man spricht von voreilen und nacheilen

Anmerkung: Der Masstab der Geschwindigkeit wurde so gewählt, dass die beiden Amplituden gleich gross erscheinen.
Beschleunigung
Eine dritte Möglichkeit zur Beschreibung der Vibration ist die Beschleunigung
Die Beschleunigung ist sinusförmig wie der Schwingweg. Sie zeigt jedoch genau in die entgegen gesetzte Richtung.
Wir können auch sagen:
Die Beschleunigung eilt dem Schwing-weg um eine halbe Periode voraus.
Der Phasenwinkel beträgt 180°
A = Beschleunigungs-Amplitude
Frequenz f = 1/T

Anmerkung: Der Masstab der Beschleunigung wurde so gewählt, dass die beiden Amplituden gleich gross erscheinen.
Beziehung zwischen Beschleunigung, Geschwindigkeit und Weg
Bis dahin haben wir alle Amplituden auf "eine Einheit" gesetzt, d.h. wir haben den Masstab der gezeichneten Kurven derart gewählt, dass sie einheitlich mit der selben Amplitude erscheinen. Es war dadurch etwas einfacher die Eigenschaften der sinusförmigen Vibration und im speziellen die Phasenlage von a, v und d zu verstehen.
Die Amplituden von Beschleunigung, Geschwindigkeit und Schwingweg stehen jedoch immer in einem bestimmten Verhältnis zueinander, welches von der Frequenz abhängig ist.
Im Folgenden wollen wir dieses Gesetz genauer anschauen.
Bei einer harmonischen Schwingung können wir nebst der Frequenz nur eine Amplitude (z.B. die Beschleunigung) wählen. Mit dieser Wahl sind die andern Amplituden (von Geschwindigkeit und Weg) in einer fixen Relation vorgegeben.
Bei konstanter Beschleunigung A und steigender Frequenz f sinkt die Geschwindigkeit V umgekehrt proportional zu der Frequenz:
Der Schwingweg ist umgekehrt pro- portional zu der Frequenz im Quadrat:
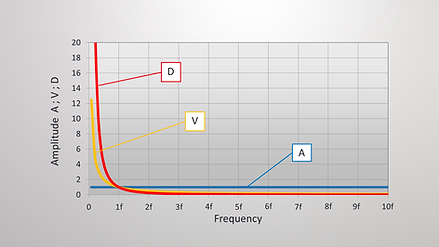
Für tiefe Frequenzen werden die Werte für v und d sehr gross und für hohe Frequenzen sehr klein.
Aus diesem Grund verwenden wir meist logarithmische Skalen für die Frequenz und die Amplituden
Eine logarithmische Skala ist nicht-linear. Die Werte von einer Teilung zur nächsten erhöhen sich jeweils um einen bestimmten Faktor, zum Beispiel Faktor 10 wie auf der Graphik rechts.
Dies erlaubt eine Darstellung der Werte über mehrere Dekaden.

Die Amplitude der Geschwindigkeit verringert sich um -1 Dekade pro Dekade der Frequenz
und die Amplitude des Schwingwegs verringert sich um -2 Dekaden pro Dekade der Frequenz.
Dimensionen von Schwingbeschleunigung, -geschwindigkeit und -weg
Im Kapitel über die gleichförmige Beschleunigung haben wir die Dimensionen der Vibrationsparameter kennen gelernt. Sie lauten für
Schwingweg : Meter (m) oder milli-Meter (mm)
Geschwindigkeit : Meter pro Sekunde (m/s) oder milli-Meter pro Sekunde (mm/s)
Beschleunigung : Meter pro Sekunde pro Sekunde (m/s²)
Dies sind gemäss dem SI-System auch die korrekten Dimensionen für die Vibrationsterme.
( = Internationales Einheitssystem)
Es wird jedoch in weiten Teilen der Industrie, vor allem im Bereich der Aeronautik, ein englisches Sysem mit folgenden Einheiten verwendet:
Schwingweg : inch (in) oder mils (in/1000)
Geschwindigkeit : inch/second (ips)
Beschleunigung : g ( = Erdbeschleunigung)
1g = 9,81 m/s²
Eine zusätzliche Eigenheit ist, dass der Schwingweg normalerweise in "Spitze-Spitze" bezw. "peak to peak" (pk-pk) Werten angegeben wird, die Geschwindigkeit und Beschleunigung dagegen in "Spitze" bezw. "peak" (pk) Werten.


